Autoevaluación
4ºParcial Diario #2 Sábado 12 Agosto 2023
Al proceso
antiderivadas se le llama integración y la familia de funciones y la familia de
las funciones que tienen este proceso se llaman integrales indefinidas.
NOTA:
Cuando resuelvan una integral indefinida siempre vamos a terminar +C.
∫2xdx
2 ∫xdx = 2x²/2+c
=2x²/2+c
=x²+c
∫2/t² dt
2∫1/t²
dt
2t-²dt
-2/t+c
♦Notación de Sumatoria
Las integrales definidas se caracterizan por resultar en un valor específico o definido. Para encontrar la integral definida de una función, tenemos que evaluar a la integral usando los límites de integración. La integral en el límite inferior es restada de la integral en el límite superior.
Proceso usado para encontrar la integral definida de una función
Supongamos que tenemos la integral . Cuando resolvemos esta integral, no obtenemos un valor específico, sino que obtenemos una función de x.
Si es que queremos obtener un valor específico para , tenemos que evaluarla en intervalos específicos. Entonces, tenemos:
Esto se escribe como
es una integral definida, ya que nos da una respuesta definitiva.
- indica que la función debe integrarse con respecto a x.
- La constante es el límite inferior de la integral.
- La constante es el límite superior de la integral.
Entonces, si es que queremos resolver la integral , seguimos los siguientes pasos:
Paso 1: Encontrar la integral de la función y usar corchetes para encerrar a la expresión integrada y para expresar los límites de integración. En este caso, tenemos:
Paso 2: Evaluar a la función en sus límites superior e inferior. La función en el límite superior es restada de la función en el límite inferior. Entonces, tenemos:
Paso 3: Simplificar hasta obtener un único valor numérico:
Calculo de area entre 2 figuras
Área de dos figuras dado funciones e igual a (f) de (x) integrables en un intervalo [a, b] de la región limitad el f’(x) y la recta es igual a y x es igual b.
INTEGRACION POR CAMBIO DE VARIABLE
El método general para realizar la integración por cambio de variable es el siguiente:
Elegir un cambio de variable que permita cambiar todos los términos y facilitar al máximo la integral.
Diferenciar el cambio de variable, de forma que podamos cambiar el diferencial.
Realizar el cambio de variable.
Completar la integral.
Deshacer el cambio de variable.
∫6x-5/3x²-5xdx
∫du/u
∫1/udu
U=3x²-5 =inu+c
du=6x-5 =in3x²-5x+c
Calculo del loguitud de arco
la longitud del arco: como la distancia que recorrías si estuvieras caminando por el camino de la curva. Muchas aplicaciones del mundo real implican la longitud del arco. Si se lanza un cohete a lo largo de una trayectoria parabólica, tal vez queramos saber hasta dónde viaja el cohete. O bien, si una curva en un mapa representa una carretera, podríamos querer saber hasta dónde tenemos que conducir para llegar a nuestro destino.
La longitud de arco es la medida de la distancia o camino recorrido a lo largo de una curva o dimensión lineal. Las primeras mediciones se hicieron posibles a través de aproximaciones trazando un polígono dentro de la curva y calculando la longitud de los lados de éste para obtener un valor aproximado de la longitud de la curva.
5) Hallar la longitud del arco de curva de la función
24xy - x4 - 48 = 0
comprendido entre los valores x = 2 y x = 4
Despejando la variable y podemos obtener la ecuación
explícita de la curva que es
Calcule la integral de , es decir,
Al aplicar el método de integración por partes, la escogencia de los factores y
es de vital importancia para calcular la integral propuesta, escojamos en este caso

Al estar definidos cada uno de los elementos del método de integración por partes, tenemos que

Sólo resta calcular la integral que está en el lado derecho de la igualdad, es decir,
Una vez que hemos calculado esta integral, sustituimos su resultado donde corresponde para obtener que
Nota: Se invita a lector a verificar si el calculo de la integral es más simple o más complicado con otra escogencia de factores.
Fracciones Parciales
y aplicamos alguna t´ecnica que nos permita encontrar los valores de las constantes, por ejemplo multiplicar por el denominador
2x − 1 = A (x − 2) (2x − 3) + B (x − 1) (2x − 3) + C (x − 1) (x − 2)
evaluando tal igualdad en x = 1 obtenemos
2 − 1 = A (1 − 2) (2 − 3) + B · 0 + C · 0
asi
Integracion de Potencias de Funciones Trigonometricas
La verdad es un buen maestro que sinceramente a pesar
de su edad sabe mucho en cuestión de cálculo, se es muy rápido lo que nos
explica ya es solo un dia a la semana en 2 horas no se puede aprender de tan
magnitud lo son los cálculos diferencial el cual no toca investigar y estudiar
a cada uno de nosotros
Pero ejercicios que, si seriamente están muy complejos,
digo a nivel personal que e buscado en YouTube ejercicios parecido no encuentro
ejemplos de las tarea que usted nos deja,
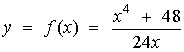
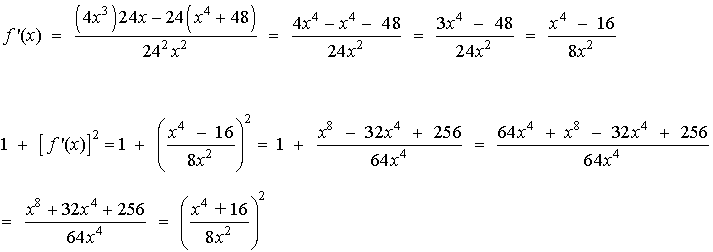


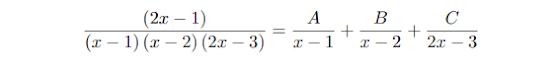






Comentarios
Publicar un comentario