Limites Trigonométricas y límites al Infinito

Limites Trigonométricas y límites al Infinito

Diario #4 Sabado 18 Febrero 2023

Este tema se me fue mas didificl entender se me complico poco mas en los limites trigonometricas

el infinito ya con unos videos como que ya me esta quedando poco mas claro....

Limites Trigonométricas

Los limites trigonometricos se dan al hacer uso de las identidades trigonometricas en una funcion y que esta la vez tienda hacia cero.

El desarollo de un limite trigonometrico puede ser resultado mediante limites notables o propiedades basica de la identidades trigonometricas

Ejercio#1:

Ejercio#2

Ejercio#3

Ejercio #4

límites al Infinito

Se dice que existe límite infinito cuando la función f(x) llega a valores que crecen continuamente, es decir que se puede hacer la función tan grande como queramos. Se dice que f(x) diverge a infinito. Para ello, el valor al que tienda la variable independiente x puede ser tanto a un número finito, como tender al infinito (límites al infinito).

Veamos un caso, con un límite infinito en la siguiente función:

Su límite cuando la variable tiende a 2 es:

Se puede comprobar si damos valores a la x cada vez más cercanos a 2, tanto acercándonos por su izquierda como por su derecha, como se ve en el siguiente cuadro, el límite tiende a +∞:

Visto en esta gráfica:

Dibujo de la gráfica en el ejemplo 1 de límites infinitos

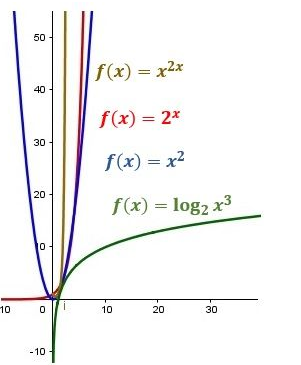
Unas funciones con un límite infinito pueden crecer más rápidamente que otras, conforme la variable x se acerca al valor del límite. Decimos que hay diferentes órdenes de infinito, según su rapidez en acercarse a él.

Comparación de órdenes de infinito en infinitos fundamentales, ordenados de mayor a menor. Para eso, veamos estas gráficas:

Sus órdenes de infinito, de mayor a menor:

Pondremos ahora las denominaciones de las funciones fundamentales, ordenadas.

Potencial exponencial > exponencial > potencial > logarítmica.

O, lo que es lo mismo:

Una función f(x) puede tener un límite infinito cuando la función f(x) llega a valores que crecen continuamente, es decir que se puede hacer la función tan grande como queramos. Se dice entonces que f(x) diverge a infinito. Esto puede ocurrir cuando la variable x tienda a un valor finito a o también cuando x tienda al infinito. Veamos los tipos que se pueden presentar.

Tipos de límites infinitos

Veamos cómo calcular la indeterminación infinito menos infinito en una función con fracciones resolviendo un ejemplo paso a paso:

$\displaystyle \lim_{x \to +\infty} \left( \frac{x^2}{x-1} - \frac{x}{3}\right)$

Primero intentamos calcular el límite:

$\displaystyle \lim_{x \to +\infty}\left( \frac{x^2}{x-1} - \frac{x}{3}\right) = \frac{(+\infty)^2}{(+\infty)-1} - \frac{+\infty}{3} = \bm{+\infty - \infty}$

Pero obtenemos la indeterminación ∞-∞.

De modo que primero debemos hacer la resta de las fracciones. Para ello, reducimos las fracciones a común denominador, esto es, multiplicamos el numerador y el denominador de una fracción por el denominador de la otra:

$\begin{array}{l}\displaystyle\lim_{x \to +\infty} \left( \frac{x^2}{x-1}-\frac{x}{3}\right)=\\[5ex]\displaystyle =\lim_{x \to +\infty}\left(\frac{x^2 \cdot 3}{(x-1)\cdot 3}- \frac{x\cdot (x-1)}{3\cdot (x-1)} \right)=\\[5ex]\displaystyle = \lim_{x \to +\infty} \left( \frac{3x^2 }{3(x-1)}- \frac{x^2-x}{3(x-1)}\right)\end{array}$