FRACCIONES PARACIALES
Fracciones Parciales
3ºParcial Diario #2 Sábado 15 Julio 2023
Este método permite integrar algunas de las
funciones racionales, que difícilmente se pueden
resolver mediante otros métodos de integración.
La integración por fracciones parciales es un método
algebraico que permite descomponer una fracción
racional en la suma de varias fracciones
uso de las fracciones parciales ha permitido solucionar múltiples problemas en el Algebra Superior y de ahí su importancia en
aprenderlas. El presente manual tiene como objetivo iniciar su estudio, el cual se logrará en función de los ejercicios resueltos que se
propone
1. Cuando el ‘denominador’ de la fracción es de primer grado
y no está repetido
en donde, A, B, C son el contenido a determinarse
3. Cuando el ‘denominador’ de la fracción es de segundo grado
y no está repetido
donde A y B son las constantes a determinarse.
4. Cuando el ‘denominador’ de la fracción es de segundo grado
y está repetido
donde A, B, C, D, E, F son constantes a determinarse.
1. Analizar la Fracción Parcial: Se verifica que el polinomio del numerador sea de menor grado que el denominador. En caso de
no serlo se transforma la fracción a una forma mixta, usando el
Teorema de la División (Prueba de la división).
2. Factorar el denominador si no lo está. Siempre es conveniente tener
el denominador en su forma factorada.
3. Determinar las constantes. Dependiendo del sistema de ecuaciones que se obtenga se procede a resolverlo para determinar el
valor de las constantes del sistema.
4. Reemplazar las constantes. Finalmente se sustituyen los valores de
las constantes determinadas para la expresión
Ejercicios
Como ya conocemos las ra´ıces del denominador, efectuamos la descomposici´on en fracciones parciales
y aplicamos alguna t´ecnica que nos permita encontrar los valores de las constantes, por ejemplo multiplicar por el denominador
2x − 1 = A (x − 2) (2x − 3) + B (x − 1) (2x − 3) + C (x − 1) (x − 2)
evaluando tal igualdad en x = 1 obtenemos
2 − 1 = A (1 − 2) (2 − 3) + B · 0 + C · 0
asi
1 = A (−1) (−1) =⇒ A = 1
evaluando en x = 2 se obtiene
4 − 1 = A · 0 + B (2 − 1) (4 − 3) + C · 0
as´ı
3 = B
y finalmente, evaluando en x =
3 /2
se obtiene
asi
Referencia:






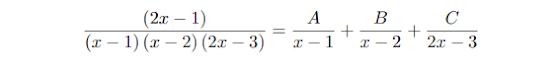







Comentarios
Publicar un comentario