Maximo y Minimo
Determinacion de maximo y minimo
3º Parcial Diario #2 Sábado 1 Abril 2023
En tema que miramos el sabado
En esta sección, aprenderás cómo se relacionan los valores máximos y mínimos de las funciones (llamados extremos) con las derivadas.
Concepto
Poder distinguir los valores más pequeños y más grandes de una función y dónde es que ocurren en cierto intervalo del dominio o sobre todo el dominio es de gran utilidad al momento de graficar una ecuación de una función y también para resolver problemas de “optimización”. La ubicación de estos extremos se vincula con el comportamiento de la derivada.
Ejemplo para sacar un punto máximo y mínimo de una función
1ER PASO
Se saca la derivada de la función:
f'(x)= 3x^2 - 6x - 9
3x^2 - 6x - 9 = 0
Se ^puede dividir entre 3 y queda:
x^2 - 2x - 3= 0
Se factoriza:
(x - 3)(x+ 1) = 0
x-3 = 0 ; x + 1=0
x= 3 ; x= -1
Estos son los valores para x de los máximos y mínimos, pero ahora toca saber cuál es cual.
2DO PASO
Se saca una segunda derivada y queda así:
f''(x) = 6x - 6
y se evalúan con las dos x que despejamos.
f''(-1) = 6(-1) - 6= - 12. Como el resultado es menor que 0, el valor evaluado representa un máximo.
f''(3)= 6(3) - 6= + 12 . Como el resultado es mayor que 0, el valor evaluado representa un mínimo.
Ahora, con los valores de x despejados, se evalúa en la función original para sacar el valor de y del máximo y del mínimo:
f(-1)= (-1)^3 - 3(-1)^2 - 9(-1) + 1= -1 -3 + 9 + 1= 6
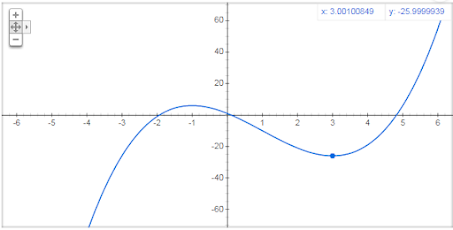
f(3) = (3)^3 - 3(3)^2 - 9(3) + 1= 27 -27 - 27 +1= -26
Con esto ya sabemos las coordenadas para los valores máximos y mínimos de la función.
V. Máx: (-1 , 6) V. Mín:(3 , - 26)
PASO 3
A se saca el punto de inflexión para saber donde cambia la curvatura entre los puntos máximos y mínimos.
La segunda derivada se iguala a cero para sacar el valor que queremos al despejar la x.
6x - 6 = 0
6x= 6
x=6/6
x= 1
Luego se sustituye este valor en la función original para sacar el valor de y.
f(1)= (1)^3 -3(1)^2 - 9(1) +1
f(1)= 1 -3 -9 +1 = - 10
Y aquí la tenemos, la coordenada del punto de inflexión es (1, - 10).
En este punto la derivada atraviesa la función.
Referencias:
CÁLCULO DIFERENCIAL - MÁXIMOS Y MÍNIMOS (weebly.com)
Cómo encontrar los máximos y mínimos (extremos) de las funciones | CK-12 Foundation (ck12.org)
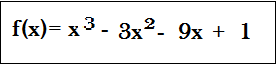



Comentarios
Publicar un comentario