Reglas de las derivadas trigonométricas

Reglas de la derivadas algebraicas

2º Parcial Diario #3 Sábado 11 Marzo 2023

Sábado ya en las clases presencial Continuamos con las derivadas de las dos mas de las reglas de las derivadas algebraicas, que nos hicieron falta

Ahora ya empezamos a ver derivadas trigonométricas que esas para mi son poco más Difíciles de entender cuando aplicamos seno es igual coseno. Ahora es aprenderme las reglas trigonométricas para sea más fácil

Regla #6 Derivada conciente

la derivada del cociente de dos funciones es igual a la derivada del numerador por el denominador menos la derivada del denominador por el numerador, divididas por el cuadrado del denominador.

Regla #7 Derivada de la Cadena

La Regla de la cadena es una norma de la derivacion que nos dice que, teniendo una variable y que depende de u, y si depende a la variable x, entonces la razon de cambio de y respecto a x puede estimarse como el producto de la derivada de y cib respecto a u por la derivada de u respecto a x.

La regla de la cadena sirve para derivar la composición de funciones.

La derivada de la composición es

Enunciamos las reglas de derivación y de la cadena y proporcionamos algunos ejemplos de su aplicación. Derivadas. Cálculo diferencial. Matemáticas.

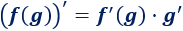
Es decir,

Enunciamos las reglas de derivación y de la cadena y proporcionamos algunos ejemplos de su aplicación. Derivadas. Cálculo diferencial. Matemáticas.

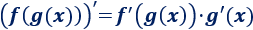
Ejemplo 1

Sea la función

Enunciamos las reglas de derivación y de la cadena y proporcionamos algunos ejemplos de su aplicación. Derivadas. Cálculo diferencial. Matemáticas.

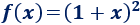
Es composición de las siguientes funciones:

Enunciamos las reglas de derivación y de la cadena y proporcionamos algunos ejemplos de su aplicación. Derivadas. Cálculo diferencial. Matemáticas.

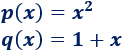
ya que

Enunciamos las reglas de derivación y de la cadena y proporcionamos algunos ejemplos de su aplicación. Derivadas. Cálculo diferencial. Matemáticas.

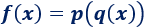
O, equivalentemente, $f = p (q)$ .

Las derivadas son

Enunciamos las reglas de derivación y de la cadena y proporcionamos algunos ejemplos de su aplicación. Derivadas. Cálculo diferencial. Matemáticas.

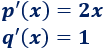
Por tanto, por la regla de la cadena,

Enunciamos las reglas de derivación y de la cadena y proporcionamos algunos ejemplos de su aplicación. Derivadas. Cálculo diferencial. Matemáticas.

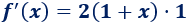
Ejemplo 2

Enunciamos las reglas de derivación y de la cadena y proporcionamos algunos ejemplos de su aplicación. Derivadas. Cálculo diferencial. Matemáticas.

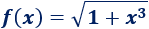
Si es necesario, se puede escribir la raíz como una potencia con exponente $1 / 2$ .

Aplicando la regla de la cadena,

Enunciamos las reglas de derivación y de la cadena y proporcionamos algunos ejemplos de su aplicación. Derivadas. Cálculo diferencial. Matemáticas.

Reglas de la derivadas Trigonometricas

Las derivadas de funciones trigonométricas son otras funciones trigonométricas. Por ejemplo, la derivada de la función seno es igual a la función coseno y la derivada de la función coseno es igual a seno negativo.

A continuación, conoceremos todas las fórmulas de las derivadas de las funciones trigonométricas. Además, veremos algunos ejercicios en donde aplicaremos estas fórmulas.

Derivada de la función seno

$f(x)=\sin(u) \ \ \Longrightarrow \ \ f'(x)=\cos(u)\cdot u'$

Derivada de la función coseno

$f(x)=\cos(u) \ \ \Longrightarrow \ \ f'(x)=-\sin(u)\cdot u'$

Derivada de la función tangente

$f(x)=\tan(u) \ \ \Longrightarrow \ \ f'(x)=\sec^{2}(u)\cdot u'$ </>

Derivada de la función cotangente

$f(x)=\cot(u) \ \ \Longrightarrow \ \ f'(x)=-\csc^{2}(u)\cdot u'$

Derivada de la función secante

$f(x)=\sec(u) \ \ \Longrightarrow \ \ f'(x)=\sec(u)\cdot \tan(u)\cdot u'$

Derivada de la función cosecante

$f(x)=\csc(u) \ \ \Longrightarrow \ \ f'(x)=-\csc(u)\cdot \cot(u)\cdot u'$

Ejercicios

Deriva las siguientes funciónes

Recuerda siempre derivar el argumento de la función trigonométrica y multiplicarlo por la derivada de la función.

1 $f(x)=\sin(4x)$

aPrimero hacemos $u=4x$

bCalculamos la derivada de $u$

$u'=4$

cSustituimos en la fórmula de la derivada del seno

$f'(x)=\cos(4x)\cdot 4$

dReordenando se tiene

$f'(x)=4\cos(4x)$

2 $f(x)=\sin(x^{4})$

aPrimero hacemos $u=x^4$

bCalculamos la derivada de $u$

$u'=4x^3$

cSustituimos en la fórmula de la derivada del seno

$f'(x)=\cos(x^4)\cdot 4x^3$

dReordenando se tiene

$f'(x)=4x^3\cos(x^4)$

3 $f(x)=\sin^{4}(x)=(\sin(x))^{4}$

aPrimero hacemos $u=\sin x$

bCalculamos la derivada de $u$

$u'=\cos (x)$

cSustituimos en la fórmula de la derivada de la función potencia

$f'(x)=4\sin^3(x)\cdot \cos(x)$

4 $f(x)=\cfrac{cos(x)}{5}=\cfrac{1}{5}\cdot cos(x)$

aPrimero hacemos $u=x$

bCalculamos la derivada de $u$

$u'=1$

cSustituimos en la fórmula de la derivada del coseno

$f'(x)=-\cfrac{1}{5}\sin(x)\cdot 1$

dReordenando se tiene

$f'(x)=-\cfrac{1}{5}\sin(x)$

5 $f(x)=\cos(3x^{2}+x-1)$

aPrimero hacemos $u=3x^2+x-1$

bCalculamos la derivada de $u$

$u'=6x+1$

cSustituimos en la fórmula de la derivada del coseno

$f'(x)=-\sin(3x^2+x-1)\cdot (6x+1)$

dReordenando se tiene

$f'(x)=-(6x+1)\sin(3x^2+x-1)$

6 $f(x)=\cfrac{1}{2}\cdot cos^{2}(5x)$

aPrimero hacemos $u=\cos(5x)$

bCalculamos la derivada de $u$

$u'=-5\sin(5x)$

cSustituimos en la fórmula de la derivada de la función potencia

$f'(x)=\cfrac{1}{2}\cdot 2\cos(5x)\cdot (-5\sin(5x))$

dReordenando se tiene

$f'(x)=-5\cos(5x)\cdot\sin(5x)$

7 $f(x)=tan\sqrt{x}$

aPrimero hacemos $u=\sqrt{x}$

bCalculamos la derivada de $u$

$u'=\cfrac{1}{2\sqrt{x}}$

cSustituimos en la fórmula de la derivada de la tangente

$f'(x)=\sec^2\sqrt{x}\cdot \cfrac{1}{2\sqrt{x}}$

dReordenando se tiene

$f'(x)=\cfrac{\sec^2\sqrt{x}}{2\sqrt{x}}$

8 $f(x)=cot(4x^{2})$

aPrimero hacemos $u=4x^2$

bCalculamos la derivada de $u$

$u'=8x$

cSustituimos en la fórmula de la derivada de cotangente

$f'(x)=-\csc^2(4x^2)\cdot 8x$

dReordenando se tiene

$f'(x)=-8x\csc^2(4x^2)$

9 $f(x)=cot^{2}(4x)$

aPrimero hacemos $u=cot(4x)$

bCalculamos la derivada de $u$

$u'=-4\csc^2(4x)$

cSustituimos en la fórmula de la derivada de la función potencia

$f'(x)=2\, cot(4x)\cdot (-4\csc^2(4x))$

dReordenando se tiene

$f'(x)=-8\, cot(4x)\cdot\csc^2(4x)$

10 $f(x)=sec(5x)$

aPrimero hacemos $u=5x$

bCalculamos la derivada de $u$

$u'=5$

cSustituimos en la fórmula de la derivada de secante

$f'(x)=\sec(5x)\cdot tan(5x)\cdot 5$

dReordenando se tiene

$f'(x)=5\sec(5x)\cdot tan(5x)$

11 $f(x)=csc\left (\cfrac{x}{2} \right )$

aPrimero hacemos $u=x/2$

bCalculamos la derivada de $u$

$u'=1/2$

cSustituimos en la fórmula de la derivada de cosecante

$f'(x)=-\csc\left(\cfrac{x}{2}\right)\cdot cot\left(\cfrac{x}{2}\right)\cdot\cfrac{1}{2}$

dReordenando se tiene

$f'(x)=-\cfrac{1}{2}\csc\left(\cfrac{x}{2}\right)\cdot cot\left(\cfrac{x}{2}\right)$

referencias:

Derivada de un cociente | Superprof

Regla de la cadena - Qué es, definición y concepto | 2023 | Economipedia

Derivada de las funciones trigonometricas | Superprof

Buscar este blog

Monnyka Oseguera