Conocimiento previo
Conocimiento previo
Limites por factorización y Racionalización
Ley de Signos
Ejemplo Multiplicación
(26)
x (-13) =338 Recuerda que dos signos diferentes
te darán un numero negativo de resultado.
(25)
x (25) = 625 Recuerda que dos signos iguales te darán
un numero positivo de resultados.
Nota
importante: La ley de los signos se aplica de la misma manera en
multiplicaciones y divisiones.
Ejemplo
de sumas
14+17=31 Ambos
signos son positivos, realizamos una suma como lo hemos hecho siempre.
(-6) +(-2) =-8 Cuando
son dos signos negativos se suman y se escribe el mismo signo negativo.
(-7) + 4 =
-3 Cuando el primer número sea negativo y el segundo
positivo lo resta y escribes el signo negativo
Nota importante:
- En
suma, de números positivos con números positivos, el resultado es un
número positivo.
- De
ser una suma de un número negativo con otro número negativo, el resultado
es negativo.
- Si
se trata de un número positivo con un número negativo el signo en el
resultado es del número entero de mayor valor.
Ejemplo de Restas:
6 – 4 = 2 Ambos signos son positivos y el resultado siempre dará positivo
( -7) – (-4) = - 3 Ambos signos son negativos, se restan y se escribe el mismo signo negativo.
Nota importante:
se debe tomar en cuenta que si un numero no posee un signo evidente este se sobre entiende que es de signo positivo + y no es necesario escribirlo. En el caso de ser un resultado negativo, se necesita escribir el signo negativo.
Formula General
![]()
Para resolver ecuaciones de segundo grado usando la fórmula general, primero debemos identificar los valores de los coeficientes.
Ejemplos:
1 ![]()
1 identificamos los valores de a, b y c
![]()
2 sustituimos en la fórmula general y resolvemos

![]()
![]()
![]()

3La ecuación tiene dos soluciones reales distintas
![]()
Este tipo de indeterminación se suele
n
presentar en cocientes de polinomios; cuando calculamos limites en un punto en
el que se nos anula tanto el numerador como el denominador. Para resolver la indeterminación
hay que descomponer en factores los polinomios, tanto del Numerados como
Denominador (utilizando Ruffini, ecuaciones de segundo grado, productos notables)
y se genera el factor nulo en numerador y denominador, que al simplicarlo conduce a la resolución de la indeterminación
aparece asociada a raíces, binomios de raíces, se hace necesario multiplicar y
dividir por el conjugado del binomio de raíces para que “ asome” el factor nulo.
En esta nuevo sección de operaciones algebraicas, desarrollaremos la multiplicación algebraica donde multiplicaremos factores algebraicos obteniéndose como resultado otra expresión llamado producto.
La multiplicación entre expresiones es independiente de la existencia de términos semejantes, esto solo es aplicable cuando tratamos con la suma y resta algebraica.
Aquellas proposiciones que ya hemos demostrado previamente serán usadas en esta sección. Estas leyes son la ley de los signos, las leyes de la potenciación de la teoría de exponentes como las leyes distributivas de multiplicación con respecto a la suma y resta.
Leyes de exponentes para la multiplicación
Por tratarse de un curso elemental de álgebra, necesitaremos las propiedades de teoría de exponentes ya anteriormente estudiadas. Por tratarse de multiplicación entre polinomios, usaremos las 3 principales leyes de la potenciacion para la multiplicación y son:
Multiplicación de potencias de bases iguales
Potencia de un producto
Potencia de potencia
Multiplicación entre monomios
La multiplicación entre monomios es muy sencilla:
- Primero multiplicamos los coeficientes de cada monomio
- Luego multiplicamos la parte literal, esto es, las variables según las leyes de los exponentes que estudiamos anteriormente.
- Aplicamos las ley distributiva
- Por ultimo aplicamos finalmente la leyes de los signos.
El siguiente diagrama para indica las partes de un monomio.
Ejemplo
Multiplicación de monomio por un polinomio
Para realizar la multiplicación de un monomio por un polinomio, aplicaremos la ley distributiva, esto es, se multiplica el monomio a cada termino del polinomio, luego, realizar el proceso de multiplicación entre monomios que ya explicamos anteriormente.
Este tipo de multiplicación tiene la siguiente forma , donde , y son monomios., veamos algunos ejemplos aclaratorios.
Ejemplos
Multiplicación entre polinomios
Para saber como resolver la multiplicación entre polinomios, tan solo debemos tener en cuneta la propiedad distributiva, la ley se signos y las leyes de la potenciación.
La forma mas básica o reducida de la multiplicación entre dos polinomio es de la forma , esto es, la multiplicación entre dos binomios, su prueba es muy sencilla, es tan solo aplicando la propiedad distributiva. Veamos, la propiedad nos dice que , si suponemos que , y , remplazando en la propiedad, tenemos:
Por lo general, llamamos multiplicando al factor de la izquierda y multiplicador al factor de la derecha , esto es:
Factorizar una expresión o un número significa escribir esa expresión o ese número como una multiplicación de factores. Entonces, factorizar es lo inverso de la multiplicación. Cuando multiplicamos, escribimos:
Pero, si es que factorizamos, escribimos:
Aquí factorizamos a ya que lo escribimos como el producto .
En la suma , 5 es un factor común de cada término. El 5 es un factor de y también un factor de .
EJERCICIO 4
Extrae el factor común de la expresión .
En este caso, podemos ver que el factor común de ambos términos es 3x
Podemos verficar esto al multiplicar y expandir la expresión de la derecha:
Referencias:.
https://www.loscastanoselsalvadorschool.com/post/tema-1-aplicaci%C3%B3n-de-la-ley-de-los-signos





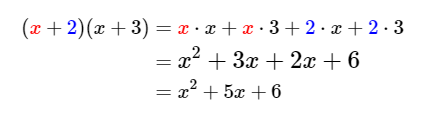



Comentarios
Publicar un comentario